Problem
Consider an undirected graph where each edge weighs 6 units. Each of the nodes is labeled consecutively from 1 to n.
You will be given a number of queries. For each query, you will be given a list of edges describing an undirected graph. After you create a representation of the graph, you must determine and report the shortest distance to each of the other nodes from a given starting position using the breadth-first search algorithm (BFS). Return an array of distances from the start node in node number order. If a node is unreachable, return -1 for that node.
Example
The following graph is based on the listed inputs:
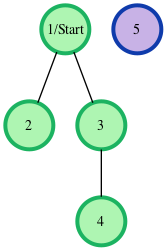
n = 5 // number of nodes
m = 3 // number of edges
edges = [1, 2], [1, 3], [3, 4]
s = 1 // starting node
All distances are from the start node 1. Outputs are calculated for distances to nodes 2 through 5: [6, 6, 12, -1]. Each edge is 6 units, and the unreachable node 5 has the required return distance of -1.
Function Description
Complete the bfs function in the editor below. If a node is unreachable, its distance is -1.
bfs has the following parameter(s):
- int n: the number of nodes
- int m: the number of edges
- int edges[m][2]: start and end nodes for edges
- int s: the node to start traversals from
Returns
int[n-1]: the distances to nodes in increasing node number order, not including the start node (-1 if a node is not reachable)
Input Format
The first line contains an integer q, the number of queries. Each of the following q sets of lines has the following format:
- The first line contains two space-separated integers n and m, the number of nodes and edges in the graph.
- Each line i of the m subsequent lines contains two space-separated integers, u and v, that describe an edge between nodes u and v.
- The last line contains a single integer, s, the node number to start from.
Constraints
- 1 ≤ q ≤ 10
- 2 ≤ n ≤ 1000
- 1 ≤ m ≤ { n*(n-1) } / 2
- 1 ≤ u, v, s ≤ n
Sample Input
2
4 2
1 2
1 3
1
3 1
2 3
2Sample Output
6 6 -1
-1 6Explanation
We perform the following two queries:
- The given graph can be represented as:
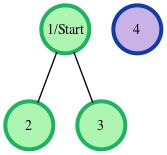
where our start node, s, is node 1. The shortest distances from s to the other nodes are one edge to node 2, one edge to node 3, and an infinite distance to node 4 (which it is not connected to). We then return an array of distances from node 1 to nodes 2, 3, and 4 (respectively): [6, 6, -1]. - The given graph can be represented as:
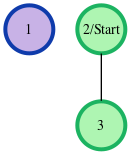
where our start node, s, is node 2. There is only one edge here, so node 1 is unreachable from node 2 and node 3 has one edge connecting it to node 2. We then return an array of distances from node 2 to nodes 1, and 3 (respectively): [-1, 6].
Note: Recall that the actual length of each edge is 6, and we return -1 as the distance to any node that is unreachable from s.
무방향 그래프에서 각 간선의 가중치는 6입니다. 각 노드는 1부터 n까지 순차적으로 번호가 매겨져 있습니다.
여러 개의 쿼리가 주어집니다. 각 쿼리마다 무방향 그래프를 나타내는 간선 리스트가 제공됩니다. 이 그래프를 나타낸 후에 BFS(너비 우선 탐색) 알고리즘을 사용하여 주어진 시작 위치에서 다른 노드들까지의 최단 거리를 계산하고 보고해야 합니다. 시작 노드에서 다른 노드들까지의 거리를 배열로 반환하며, 도달할 수 없는 노드의 거리는 -1로 나타냅니다.
예제
- 노드 개수: n = 5
- 간선 개수: m = 3
- 간선 목록: [1, 2], [1, 3], [3, 4]
- 시작 노드: s = 1
시작 노드 1에서 각 노드까지의 거리는 다음과 같습니다:
- 노드 2: 6
- 노드 3: 6
- 노드 4: 12
- 노드 5: 도달 불가 (-1)
따라서 출력은 [6, 6, 12, -1]입니다.
함수 설명
함수 bfs는 다음 매개변수를 받습니다:
- int n: 노드의 개수
- int m: 간선의 개수
- List<List<Integer>> edges: 간선의 시작 및 끝 노드를 나타내는 2차원 리스트
- int s: 탐색을 시작할 노드
반환값: 길이가 n-1인 리스트로, 시작 노드를 제외한 각 노드까지의 거리를 반환합니다. 도달할 수 없는 노드는 -1로 나타냅니다.
Solution
import java.util.*;
public class Solution {
public static List<Integer> bfs(int n, int m, List<List<Integer>> edges, int s) {
// 그래프 초기화
Map<Integer, List<Integer>> graph = new HashMap<>();
for (int i = 1; i <= n; i++) {
graph.put(i, new ArrayList<>());
}
for (List<Integer> edge : edges) {
int u = edge.get(0);
int v = edge.get(1);
graph.get(u).add(v);
graph.get(v).add(u);
}
// 거리 배열 초기화
int[] distances = new int[n + 1];
Arrays.fill(distances, -1);
distances[s] = 0;
// BFS 탐색
Queue<Integer> queue = new LinkedList<>();
queue.add(s);
while (!queue.isEmpty()) {
int current = queue.poll();
for (int neighbor : graph.get(current)) {
if (distances[neighbor] == -1) {
distances[neighbor] = distances[current] + 6;
queue.add(neighbor);
}
}
}
// 결과 리스트에 거리 추가 (시작 노드 제외)
List<Integer> result = new ArrayList<>();
for (int i = 1; i <= n; i++) {
if (i != s) {
result.add(distances[i]);
}
}
return result;
}
}
- 그래프 초기화: 입력받은 edges 리스트를 사용하여 무방향 그래프를 Map<Integer, List<Integer>> 형태로 만듭니다.
- 거리 배열 초기화: 모든 노드의 거리를 -1로 설정하고, 시작 노드의 거리를 0으로 설정합니다.
- BFS 탐색: 시작 노드부터 BFS를 수행하여 각 노드까지의 최단 거리를 구합니다. BFS는 큐를 사용하며, 현재 노드와 연결된 노드 중 방문하지 않은 노드를 큐에 추가하고 거리를 업데이트합니다.
- 결과 반환: 시작 노드를 제외한 각 노드의 거리를 result 리스트에 추가하여 반환합니다.
동작 방식
BFS는 그래프의 모든 노드를 한 번씩 방문하면서 최단 거리를 찾기 때문에 각 노드까지의 최단 거리 값을 효율적으로 계산할 수 있습니다.
1. 그래프 초기화 부분
for (List<Integer> edge : edges) {
int u = edge.get(0);
int v = edge.get(1);
graph.get(u).add(v);
graph.get(v).add(u);
}여기서 edges는 각 간선을 나타내는 2차원 리스트입니다. 예를 들어 edges가 [[1, 2], [1, 3], [3, 4]]라면, 각 간선은 두 개의 노드 번호 [u, v]로 구성되어 있습니다. 각 간선이 무방향이므로, 노드 u와 v는 서로 연결되어 있음을 나타냅니다.
- edge.get(0): 현재 간선 edge에서 첫 번째 요소를 가져오는데, 이는 노드 u입니다.
- edge.get(1): 현재 간선 edge에서 두 번째 요소를 가져오는데, 이는 노드 v입니다.
그래프에 u와 v 연결하는 방법
그래프는 Map<Integer, List<Integer>> 형태로 저장되므로, u 노드의 인접 리스트(graph.get(u))에 v를 추가하고, v 노드의 인접 리스트(graph.get(v))에 u를 추가하여 양방향 연결을 저장합니다.
즉, 이 부분은 그래프를 무방향 연결 방식으로 초기화하는 역할을 합니다. 예를 들어, 노드 1과 노드 2가 연결되어 있으면 graph에서 1의 리스트에 2를, 2의 리스트에 1을 추가해 서로를 연결해주는 식입니다.
2. 거리 배열 초기화
Arrays.fill(distances, -1);
distances[s] = 0;- Arrays.fill(distances, -1);
- Arrays.fill()은 배열의 모든 요소를 지정된 값으로 초기화할 때 사용합니다. 여기서는 distances 배열의 모든 요소를 -1로 설정하여, 초기에는 모든 노드가 방문되지 않았음을 나타냅니다.
- -1로 초기화한 이유는 BFS 탐색을 통해 각 노드에 도달할 수 있는 최단 거리를 계산할 때, 아직 방문되지 않은 노드와 구별하기 위해서입니다. 나중에 BFS가 완료된 후에도 -1인 노드는 시작 노드에서 도달할 수 없는 노드로 간주됩니다.
- distances[s] = 0;
- distances 배열에서 distances[s] = 0으로 설정함으로써 시작 노드에서 자신까지의 거리는 0임을 나타냅니다. 시작 노드는 자기 자신이므로 거리는 0이 됩니다.
3. BFS 탐색을 위한 LinkedList<>
Queue<Integer> queue = new LinkedList<>();
queue.add(s);- LinkedList<>()는 자바에서 List와 Queue 인터페이스를 모두 구현하는 자료 구조로, Queue로 사용할 때는 FIFO(First In, First Out) 방식으로 작동하여 처음 들어간 요소가 가장 먼저 나옵니다.
- BFS(너비 우선 탐색)는 가까운 노드부터 차례로 탐색하므로 큐(Queue)를 사용하여 각 노드를 순서대로 탐색합니다. LinkedList는 BFS에서 자주 사용하는 큐의 자료 구조로, poll()로 가장 앞의 요소를 꺼내고, add()로 뒤에 요소를 추가할 수 있어 효율적입니다.
4. BFS 탐색 로직
BFS 알고리즘을 사용해 시작 노드로부터 각 노드까지의 최단 거리를 계산합니다.
while (!queue.isEmpty()) {
int current = queue.poll();
for (int neighbor : graph.get(current)) {
if (distances[neighbor] == -1) {
distances[neighbor] = distances[current] + 6;
queue.add(neighbor);
}
}
}- queue.poll();
- poll()은 queue에서 가장 먼저 추가된 요소를 꺼내 반환합니다. 이 요소는 현재 탐색할 노드를 나타내며, poll()을 사용하면 queue에서 해당 노드를 제거합니다.
- 탐색 과정
- for (int neighbor : graph.get(current))는 current 노드의 모든 인접 노드를 탐색하는 반복문입니다.
- if (distances[neighbor] == -1) 조건을 통해 neighbor 노드가 아직 방문되지 않았는지 확인합니다. 만약 방문된 적이 없다면, distances[neighbor]에 현재 노드에서 이동한 거리를 계산하여 저장합니다.
5. 결과 반환
List<Integer> result = new ArrayList<>();
for (int i = 1; i <= n; i++) {
if (i != s) {
result.add(distances[i]);
}
}
return result;- distances[i] 값이 -1이면 시작 노드로부터 도달할 수 없는 노드로 표시되며, 그렇지 않으면 시작 노드로부터의 최단 거리를 결과 리스트에 추가합니다.
이 전체 코드의 논리는 BFS 알고리즘을 사용하여 그래프에서 시작 노드에서 다른 모든 노드로의 최단 경로를 계산하고, 도달할 수 없는 노드는 -1로 표시하여 반환하는 방식입니다.

'코딩 테스트' 카테고리의 다른 글
| [HackerRank] Tree: Huffman Decoding (18) | 2024.11.11 |
|---|---|
| [HackerRank] Tree: Preorder Traversal (8) | 2024.11.11 |
| [HackerRank] Jesse and Cookies (0) | 2024.11.10 |
| [HackerRank] Lego Blocks (7) | 2024.11.08 |
| [HackerRank] Simple Text Editor (8) | 2024.11.07 |